Delta Force The Official Logo of Delta Force
00 PROJECTS_ 01 MEMBERS_ 02 BLOGS_
Principle of Maximum Likelihood | Part 1

01

Principle of Maximum Likelihood | Part 1

Written with ❤️ by:

Akshay Pai

Akshay Pai

Batch of 2020

Let’s face it. Machine Learning is the new fad. The big AI dream isn’t some distant dream anymore. So in this article, we’ll be going through something known as the “Principle of Maximum Likelihood ”. It’s a pretty simple principle to state, but the majority of learning algorithms in Machine Learning work because of this simple theorem.

What is it about ?

The principle of maximum likelihood is a method of obtaining the optimum values of the parameters that define a model. And while doing so, you increase the likelihood of your model reaching the “true ” model.

Okay. That probably made no sense. Let’s go through a simple example which illustrates the principle of maximum likelihood.

Now consider you have two coins; let’s call them A and B. Let the probability of getting a head with coin A be 0.5 and the probability of getting a head with coin B be 0.8. Now, let’s play a game. I randomly picked one of the two coins, tossed it three times and got 3 heads. Your job is to tell me which coin I picked.

Of course, this sounds trivial as coin B has a higher chances of landing heads. But let’s see how we would define our problem mathematically. So, we got three heads.

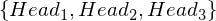
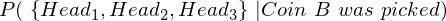
Now, we find the *conditional probabilities*

(Quick recap. Conditional probability P(A|B) gives us the probability of event A occurring **given that event B has already occurred**).

Now, since the tossing of coins is an independent event, i.e., the outcome of the first toss does not affect the outcome of the second toss, I can simplify the above equation as,

Now, computing the conditional probability for coin A is reduced to

and the conditional probability for coin B is

Now, find which conditional probability is greater, i.e., which coin has the **higher likelihood** of generating three heads consecutively. And thus, the one with the higher conditional probability gets declared as the right solution.

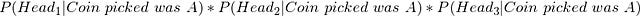
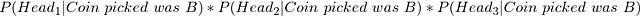
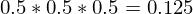
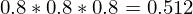
Applications in Machine Learning

Let’s now see how the principle of maximum likelihood could be applied in Machine Learning. We will be looking at two of the most fundamental supervised Machine Learning algorithms.

Consider the following example. You are given a dataset that contains the areas of houses and the prices at which those houses were purchased. That is, you have a dataset in which each entry is of the form (area, price). Now suppose you were given the area of a new house, a house that does not belong in your dataset, how would you predict the price of the house? This is done with linear regression.

But now, suppose your dataset contained the areas of houses along with a label of the house, which takes the value “0” if the house is “small” or “1” if the house is “large” (well… seems like a rather trivial task… But let’s convince ourselves that this is a rather difficult task for now). So, this kind of classification is what Logistic Regression is good for.

Linear Regression

As we just discussed, linear regression is a method of predicting future / new values given an existing dataset from which we can learn something about the correlation between different variables (in the above example, the correlation between area and price). How does it work ? Consider the following example.

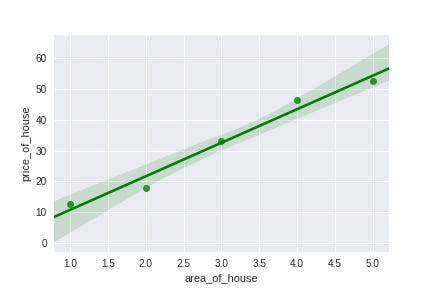
Given a set of pair-values (x,y), our objective is to find a function f which maps x to y as accurately as possible .That is, given the area of a new house, we need to accurately predict the price of the house. Let’s try plotting our dataset with house_area on the X axis and price on the Y axis.

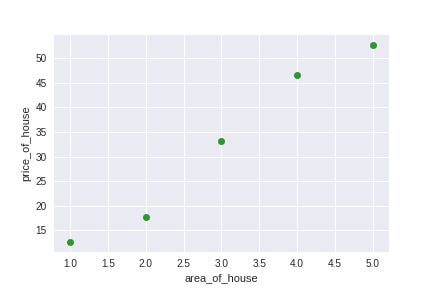
In other words , our objective is to find a function *f = m*area + c* ( I will be referring to this function as *predicted price )* so that the error between the predicted price and the actual price is minimum. This error function is also called the **cost function.** And thus, by minimizing the cost function, we obtain the best possible model for our data.

We will now describe our cost function a bit more formally. Since our cost function is the error between the prediction our model makes and the actual price of the house, we will write our cost function as

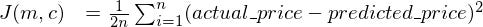
For every entry (house_area,price_of_house) in our dataset, we find the squared error between the actual price and the price we predicted, add up all of the squared errors and find the **mean squared error** . This gives us our mean error J for a given model defined by the constants *m* and *c* .

( Please note. The 1/(2n) factor is just to make the math a bit more neat. It does not affect the convex nature ( the shape ) of the cost function in any manner. So minimizing J(m,c)*k where k is some constant and obtaining the optimum values of m and c is the same as minimizing J(m,c) and obtaining m,c)

So, how do we minimize this error? Simple. Find the partial derivative of J with respect to m and the partial derivative of J with respect to c and minimize J. You could do this by gradient descent, Newton-Raphson’s or some other algorithm.

I won’t be covering their implementation in this article. But both of these find the minima of J and give you the best value of m and c. That’s how linear regression gives you the best possible function *f.*

But now the question arises: How can you be so sure that minimizing the above function will always give you the best possible parameters? That is, how can you say for sure that regardless what dataset you use, you will always arrive at the best possible values of the parameters by using the above function as your cost function ?

Let’s try defining our regression problem in a slightly different way. Now consider our earlier dataset.

Firstly, let’s assume that each of our (area_house,price_of_house) entry in our dataset is independent of each other (that is, the price of one house has nothing to do with the price of another house)

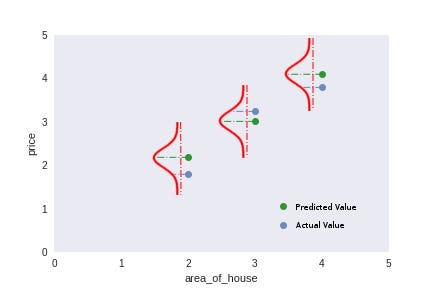
Secondly, I’m going to go ahead and assume that each entry in my dataset comes from a normal distribution centered at the prediction I make with a model and some constant standard deviation. That is; for actual_price1, I’m going to assume that it comes from a normal distribution with a mean of predicted_price1 with standard-deviation sigma. Similarly, actual_price2 comes from a distribution with mean of predicted_price2 and standard-deviation sigma and so on…

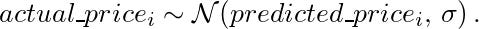
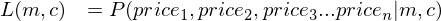
Now I’m going to define my likelihood function *L* as

Let’s break down the equation above. What L gives me is the probability of me exactly predicting the price of house1, house2… as price1, price2… given some value for m and c. So, maximizing the probability function L will give me the best possible model in the model space.

Now because of my Assumption, I can write the above expression as

or

And now, from our *Assumption 2,* since price_i comes from a normal distribution centered at the predicted_price_i, we can write each of the probability P as

Giving us

From the above expression, we see that to maximize L, we need to minimize the power of the exponent (since each product term is a probability and probability values are always greater than or equal to 0). Alternatively, one could take natural logarithm of the equation, which then results in

which is referred to as the **log likelihood.** So, we maximize the probability of getting the best model by minimizing

Since the whole expression is always greater than or equal to 0 and sigma is a constant, minimizing the above term to get values of m and c is the same as minimizing

which is the same as our cost function J(m,c). But this time, we know for a fact that minimizing J gives the the model with the maximum likelihood.

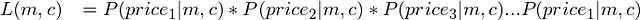
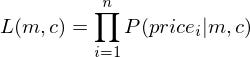
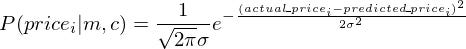
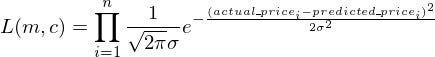
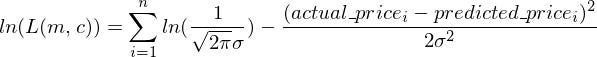
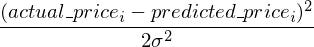
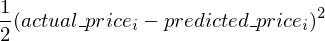
Now, you might be wondering, all of this is based on the two assumptions I made above. How can you be certain that the assumptions hold for each and every dataset you work with ? Well… you can’t. Although both the assumptions hold true for most the cases ( the second assumption due to the Central Limit Theorem and the first assumption simply because your entries are often independent of each other ), there can definitely be cases where these assumptions can be violated. So, some initial investigation into your data is always necessary before you can start running other machine learning algorithms on your dataset.

Conclusion

Well.. That brings us to the end of the part 1! In the next part, we’ll be going through how the principle of maximum likelihood can be applied to find the cost function of Logistic Regression.

Written by Akshay Pai