Nope, this is not related to AI

Programming is a moderately fun and rewarding activity, for the most part. But, have you ever looked at a piece of code and thought, “Man, I like this, but I really wish that this was crammed with a whole bunch of mathematics”? Oh, never. Well, a bunch of nerds in the computer science community, i.e., the super nerds got together in the ’50s to do just that. And so was born, functional programming, today’s new buzzword.

The beginnings

In the beginning, there was manual calculation. Then Turing said, let there be mechanization, and thus was born the Turing Machine. Then, came Alonzo Church, who said, let there be a formal system of computation built from a functional application, which led to the creation of Lambda Calculus. And thus was born from this, the functional paradigm. Although the inner workings of lambda calculus itself are not important for the conversation at hand, it is worth knowing the basics, since it forms the basis for this entire paradigm of programming. So, at a basic level, it is a mathematical model of computation that involves binding values to function parameters and applying said functions.

# Motivation

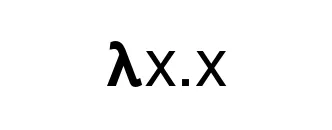
Code, while simple in theory, has a myriad of ways to manifest itself when we try and realize it in practice. There are multiple ways to define a solution for any provided task. Traditional programming, also known as imperative programming, is a model where we provide the computer with a set number of instructions to follow to accomplish the provided goal. While this has the advantage of being easy to learn and understand on a smaller scale, as the scale increases, the sheer volume can make reasoning through the code and understanding everything pretty tough, which can lead to unforeseen problems in the codebase.

The functional approach, on the other hand, aims to sidestep a lot of the problems faced by the imperative style of programming. In this style of programming, we do not provide the computer with the steps to complete a certain task, rather only describing what the program is supposed to compute.

But how do we do that? And as the name suggests, we accomplish this with the help of functions, by applying them or composing them with other functions, a throwback to its heavy mathematical influences. At its purest, a functional program consists of functions that can take in inputs and provide an output. It doesn’t have the ability to change the inputs provided or the other states of the outside calling program in any way. This pushes the functions used in this paradigm more in line with the definition of a mathematical function, and because of this, the behavior of all functions can be completely analyzed and understood, and it can also guarantee data integrity because of its immutable nature.

Now, you might be thinking, yeah, that is cool and all, but why would I want to learn a completely new set of rules when the current system works without any problems? With ever-growing technological advancements, we currently reside in a time, where storage is extremely cheap and can be easily and efficiently accessed by your programs, but the only way to increase performance is with multi-processing, which is an extremely tedious process, because of the mutability of data, which, as mentioned before, is a complete non-problem here, allowing for easy parallel processing.

There are other little improvements that it provides in the form of smaller and more understandable codebases, etc. To know about the other improvements a functional approach can provide for your development process, we will be looking at some of the other features that it provides.

Higher-Order Functions

These are functions that can take in other functions as inputs or return them as the output. This can help us generate code that is easier to understand and allow us to better reason. Here’s an example. Let us try to get the sum of an array.

As we can observe, the functional approach is much simpler and uses a higher-order function reduce, which takes in a function that sums up the numbers, starts the count at 0, and returns the sum required. Now, you might have noticed that this function inside reduce doesn’t really have a name. And that is because of the concept known as anonymous functions . They owe their origin, like most things in this paradigm to lambda calculus.

Higher-order functions also allow for some even more cool applications like currying or partial application , which is the property that allows you to only provide certain arguments to a function, which then returns a new function that already has some of its parameters bound.

As we see in the example given above, the first function takes two arguments and returns their sum as the answer. The second variable stores the partially applied function with 2, which means that the last line provides the output 5 since x is already bound. This allows us to use functions in a completely novel and useful way.

Pure functions

As previously stated, functions don’t have the ability to modify the state of the program as a whole and are said to have no side effects. This, though can seem trivial, has some pretty nice benefits attached to it.

For example, in today’s world of a constant push towards parallel processing, the immutability of data in a functional setting can alleviate a lot of the bugs that are caused by data dependencies and various other race conditions in the traditional approach. This lack of side effects also allows a compiler to better alter the ordering of the program for better efficiency since the evaluation of one is independent of another, which can lead to great efficiency improvements.

Recursion

Now, recursion, as a concept is pretty universal in nature. But they are one of the most important concepts in this paradigm since the function of a loop is accomplished with the help of recursion. In the above example, we implement a program to obtain an initial value, and then sum up all the numbers up to the given one, with the help of recursion. Now, multiple definitions of a function might seem weird at first, but this is similar to how functions are defined in mathematics, where based on the domain, we can apply a different function.

Lazy Evaluation

This is a concept where a value is not evaluated until it is necessary. For example, here

Here the first element is undefined, which, if evaluated, throws an error, but if we try to run this program, it returns 2, with no errors. This is because the values inside the array aren’t necessary to calculate the length of the array and, are hence never evaluated, hence cause no errors.

Another example, that is comparatively a bit more interesting, can be shown with the help of infinite lists .

As we can see here, the fibs list is an infinitely generated list, that starts with the values of 0 and 1, and the rest are generated in accordance with the Fibonacci sequence . The interesting thing is, even though we have asked the program to calculate an infinite list, a technically impossible feat is achieved by Haskell through the aforementioned lazy evaluation , under which, until we ask for data from the structure, none of it is ever evaluated.

Conclusion

Now, what we have discussed so far only encompasses the basics of the functional approach. But, it serves as an introduction to this new concept, that even if you don’t ever start programming in a functional language, still allows you better your code with a more functional approach wherever possible. It also allows provides you with a new set of buzzwords to brag to your friends about, so, hey, that’s great too.

The Death Of Traditional Programming